ScanSolver is a tool I made for use with the SCANSat mod in Kerbal Space Program (KSP). It is intended to help find optimal orbits for ground scanning satellites such that they complete the scan to 100% in teh shortest possible time.

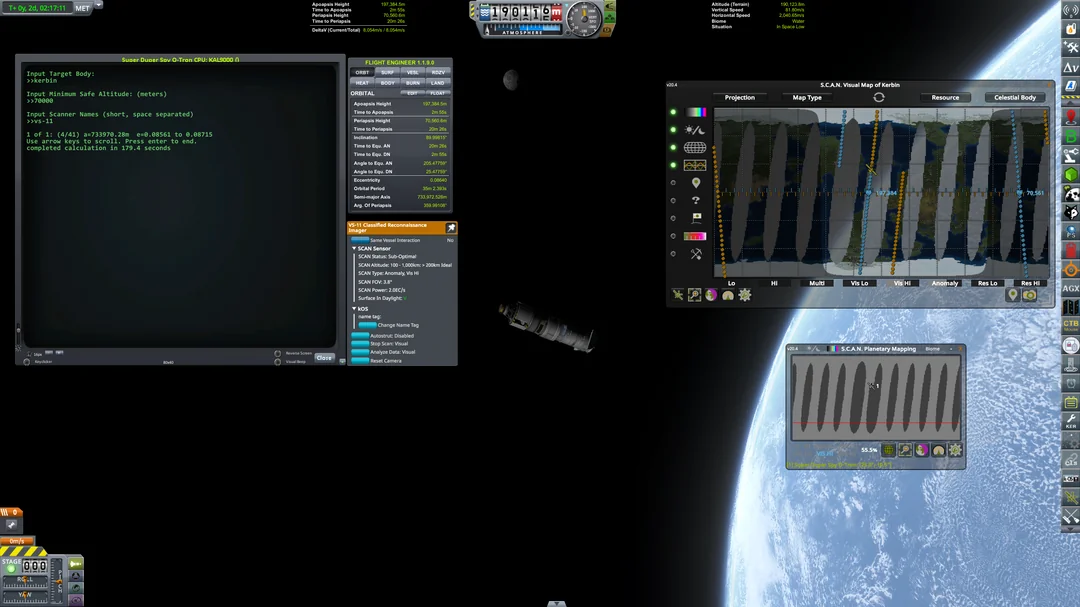
Image of a satellite in orbit with KOs terminal showing ScanSolver and the ground stacks showing on the SCANSat map

Background

SCANSat is a mod that adds various ground scanning modules for satellites to KSP. These modules can be used to map resources, image terrain, or find anomalies (easter eggs).

Each of these modules has several characteristics that impact how it performs:

  • Field of View (FoV): the typical width of the ground track in degrees(more on this later).
  • Minimum altitude: the lowest altitude at which the module can function.
  • Best altitude: poorly named, this is actually the altitude above which the FoV is maximum.
  • Maximum altitude: the maximum altitude the module will work at. Above this no data will be gathered.
  • Required daylight: Does this module require the ground to be in daylight to function.

The Field of View has some interesting behaviors that make it not quite as simple as it sounds.

  • Below “Best Altitude” FoV decreases linearly with altitude: F(A)=F0AAbestF\left(A\right) = F_0 \frac{A}{A_{best}}
  • Above “Best Altitude” FoV is constant.
  • For planets smaller than kerbin (600km radius) the FoV scales as F(R)=F0RkerbinRF(R)=F_0\sqrt{\frac{R_{kerbin}}{R}}
  • Finally, the FoV is capped at a maximum of 20 degrees

This makes the full equation for FoV

\[F\left(A, R\right)=min\left(F_0\frac{min(A, A_{best})}{A_{best}}\sqrt{\frac{R_{kerbin}}{min(R, R_{kerbin})}}, 20\right)\]

An additional thing to note is that this is the number of degrees of at the equator, at higher latitudes the track will look wider (on a square projection) as the track covers more lines of longitude as they converge to the poles.

Version 1

My first attempt at finding the best orbits kept things simple by only considering circular orbits with a perfect 90 degrees of inclination. This allows us to only consider the FoV over the equator where our track is visually the thinnest.

To find the orbit we start with the theoretical minimum number of ground tracks we will need

\[N = \lceil 180F(R)\rceil\]

and check each co-prime C of that to find an orbital period

\[T_{orbit}(C, N) = T_{day}\frac{C}{N}\]

co-primes are used to ensure the fraction CN\frac{C}{N} is irreducible, as otherwise we would end up with fewer ground tracks than intended.

We then check the altitude of that orbit and verify if it is greater than the spacing between the ground tracks. If yes, that is a valid orbit. We continue this to find the smallest value C that solves the problem, as this is the number of sidereal days that will need to pass for the scan to complete.

Version 2

This makes one major improvement over version 1 by now solving for elliptical orbits.

This allows the field of view to vary over the course of the orbit, meaning we can have the maximum field of view at the equator as needed, but complete our orbit faster by spending less time over the poles and dark side meaning our ground tracks will be closer together.

Similar to version 1, we vary our semi major axis with CN\frac{C}{N} but now we have to solve for any solutions with eccentricity.

This is done by finding the roots in e of the following equation:

\[0 = 4(a\cdot A)e^3 + R^2e^2+2(A\cdot (R - 2\cdot a))e + A^2\]

where A is the minimum altitude required over the equator, R is the radius of the body, and a is the semimajor axis of the orbit.

The full derivation of this formula was fairly complicated so I won’t go into it here.

If there is only 1 root, there are no valid orbits for this configuration. Otherwise the 2nd largest root is the minimum eccentricity and the largest root is the maximum eccentricity. These are the further constrained by limits on the eccentricity placed by being:

  • above the minimum altitude over the poles
\[e_{poles}=\sqrt{1-\frac{R+A_{min}}{a}}\]
  • above the minimum safe altitude at periapsis (eg.g maximum height of atmosphere or terrain features)
\[e_{peri}=1-\frac{R+A_{safe}}{a}\]
  • and within the maximum altitude at apoapsis
\[e_{apo} = \frac{R+A_{max}}{a} - 1\]

The rest of the process for calculation is similar to before, increase C until we hit a solution then increase N and see if we can decrease C and still get a solution. Keep going until NC\frac{N}{C} would be below the minimum altitude at all points.

Version 3

One of the assumptions that was made in version 2 was that the scan was a thin line perpendicular to the direction of travel. As this is not actually the case, there is a small amount more performance that can be gained from the effective smearing caused by the planet rotating underneath the satellite.

The base forula for Version 2 was

\[F = F_0\frac{a\frac{1-e^2}{1-ex}-R}{A_{best}}\]

to include the rotation of the planet in this we need to add a scaling factor

\[S = \frac{1}{x} + \frac{C}{N}\cdot\frac{(1-e^2)^{\frac{3}{2}}}{(1-ex)^2}\]

where xx is the cosine of the latitude the satellite is above.

We now have to solve the inequality

\[S\cdot F \ge \frac{180}{N}\]

This does not reduce to something that can be solved algebraically (at least within my skill set), so version 3 uses a numerical solver (a combination of bisection and Newton’s method).

The rest of the solver is similar in how it approaches finding the optimal solution.

This version (and version 2, though it wasn’t implemented) also allows for the output of a range of valid solutions. This gives more choice in teh orbit you choose allowing for more efficient missions, and the range or eccentricities in each solution make it easier to enter teh correct orbit accurately.

Impact, Summary, and Conclusion

Each version found significantly better solutions than the previous version. This allowed for faster scans and easier orbits.

There is still a few possibilities for improvements, the biggest of which is likely allowing for orbits that are not perfectly polar. This would allow the smearing effect to be emphasized by a retrograde orbit, further cutting down scan time. Sadly I haven’t been able to make inroads on the changes to the calculations needed for these yet (I’ve also not put much time into it).

I’ve had a lot of people give positive feedback about the tool which has continued a lot longer than expected (I assumed this would be of very niche interest). It’s alwas great to know people are using the things I put out there so if you have stories about using this I would love to hear them.